実験には誤差が伴います。誤差を加味して「真の値」を推定する際、有用な推定値を得ることができるように実験の繰り返し数を増やすことを提案します。

●真の値

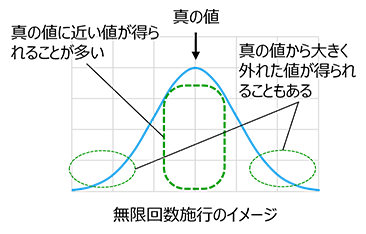
 ある条件水準で実験を無限回数施行したと仮定すると、その平均値をその条件水準における「真の値」とみなすことができます。

●真の値の推定

 ある条件水準で実験を数回数施行した場合、数値の幅をもって真の値が存在する区間を推定することができます。
 この数値の幅のことを信頼区間と言います。95％信頼区間がよく使われます。

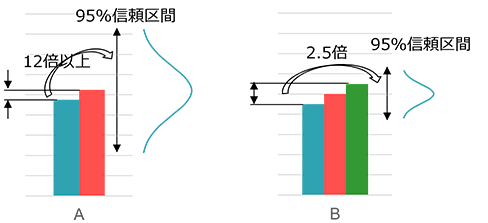
1. 2回施行の場合（A）

 95％信頼区間幅は、２つの数値の差の12倍以上になります。また真の値が2つの数値より小さい、または2つの数値より大きい確率は50％にもなります。

2. 3回施行の場合（B）

 3つの数値が等間隔のモデルケースの場合、95％信頼区間は最大値と最小値の差の2.5倍になります。この場合テータのばらつきの指標となる標準偏差は、Aよりむしろ大きくなります。

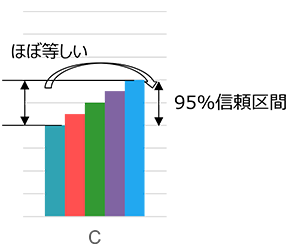
3. 5回施行の場合（C）

 5つの数値が等間隔のモデルケースの場合、95％信頼区間は最大値と最小値の差とほぼ等しくなります。
 この場合、テータのばらつきの指標となる標準偏差は、AやBよりむしろ大きくなります。

●より確からしいデータを得るため、KRIではある水準の施行回数を少なくとも3回、好ましくは5回以上を推奨します。